Advanced Excel functions offer indispensable and convenient methods for various statistical calculations and analysis. One such feature is the confidence interval, which is used to express the degree of uncertainty associated with the study. Confidence intervals in excel are an assessment of events combined with verification of probabilities. They provide the probable range of the sample proportion or the sample average of the true share / average found in the population and are displayed as: estimate +/- error.
Confidence Interval Function
In any survey and study, confidence intervals are a great way to understand the role of sampling errors in average percentages. For any survey, since researchers always only study the fraction from a larger calculation, there is uncertainty in their estimates, which will result in sampling errors.
The Confidence Interval (CI) gives an understanding of how much the average value can fluctuate. It represents a range of values that are equally centered on a known average number of samples. The higher the level of confidence (in percent), the smaller the interval, the more accurate the results. Examination of samples with greater variability or greater standard deviation generates wider confidence intervals in excel.
There is a reciprocal square root relationship between CI and sample size. Smaller sizes generate wider CIs; therefore, to obtain more accurate estimates or reduce the threshold error by half, you need to increase the sample size by about four times.
The construction of the average value of the population
To build a confidence interval for the average population value, the probability provided, and the sample size, you need to use the TRUST function in Excel, which uses the normal distribution to calculate the confidence value. Suppose the researchers randomly selected 100 people, measured their weight and set an average of 76 kg. If you need to know the average indicator for people in a particular city, it is unlikely that for a larger group it will have the same average value as a sample consisting of only 100 people.
It is much more likely that a sample average of 76 kg may be approximately equal to the (unknown) population average, and you need to know how accurate the estimated response is. This uncertainty associated with estimating the intervals is called the confidence level, usually 95%. The TRUST function (alpha, sigma, n) returns the value used to construct the CI of the average population. It is assumed that the sample data correspond to standard normal distributions with a known standard deviation sigma, and the sample size is n. Before calculating the confidence interval in the excel 95% level, take alpha as 1 - 0.95 = 0.05.
CONFIDENCE Function Formats
The CONFIDENCE or TRUST function is determined by the limits of trust - these are the lower and upper boundaries of the CI and are 95% indicators. For example, when studying preference, it was found that 70% of people prefer Borjomi compared to Pepsi with a 3% CI and a confidence level of 95%, then there is a 95% chance that the true proportion is between 67 and 73%.
The TRUST functions are displayed under various syntaxes in different versions of Excel. For example, Excel 2010 has two functions: TRUST.NORM and TRUST.T, which help calculate the width of DI. TRUST.NORM, used when the standard deviation of the measurement is known. Otherwise, "TRUST.T" is applied, the assessment is carried out according to the sample. Confidence intervals in excel until 2010 had only the TRUST function. His arguments and results were similar to those of the TRUST.NORM function.
The former is still available in later versions of Excel for compatibility. #NUM! Error - occurs if alpha is less than or equal to 0, or greater than or equal to 0. This standard deviation is less than or equal to 0. The specified argument size is less than one. #COST! Error - occurs if any of the provided arguments is not numeric.
Trust Interpolation Function
"TRUST." classified by statistics functions and will calculate and return CI for the average value. Confidence intervals in excel can be extremely useful for financial analysis. As an analyst, "TRUST." helps in forecasting and adjusting for a wide range of goals, by optimizing the adoption of financial decisions. This is accomplished by graphically displaying data in a set of variables.
Analysts can make better decisions based on statistical information provided by normal distribution. For example, they may find a connection between income earned and expenses spent on luxury goods. In order to calculate the CI for the average population value, the returned confidence value must be added and subtracted from the average value of the sample. For example, for the average sample value x: Confidence Interval = x ± TRUST.
An example of calculating the confidence interval in excel - suppose we are given the following data:
- Significance Level: 0.05.
- Population standard deviation: 2.5.
- Sample Size: 100.
The Excel Confidence Interval function is used to calculate the CI with a value of 0.05 (i.e., a confidence level of 95%) for the average sampling time to study the switching time in the office per 100 people. The average value of the sample is 30 minutes, and the standard deviation is 2.5 minutes. The confidence interval is 30 ± 0.48999, which corresponds to the range of 29.510009 and 30.48999 (minutes).
Intervals and normal distribution
The most familiar use of the confidence interval means "error of error." In polls, the margin of error is plus or minus 3%. CIs are useful in contexts that go beyond this simple situation. They can be used with abnormal distributions that are severely distorted. The following building blocks are required to calculate the confidence interval forecast in excel:
- Mean.
- Standard deviation of observations.
- The number of polls in the sample.
- The level of trust to apply to the MDI.
Before you build a confidence interval in excel, study it around the average value of the sample, begin by deciding what percentage of other sampling tools will be accepted if they were collected and calculated in this interval. If so, then 95% of the possible samples will be captured by CIs with 1.96 standard deviations above and below the sample.
Standard error of the mean
The permissible interval or error is not accepted taking into account the measurement error or the viewing bias, therefore, the actual uncertainty may be higher than indicated. Before calculating the confidence interval in excel, the calculation must be ensured by good data collection, reliable measurement systems and a satisfactory survey design.
Confidence intervals for the average value can be obtained in several ways: using SigmaXL, descriptive statistics, histograms, 1-shaped t-test and confidence intervals, one-way ANOVA and Multi-Vari diagrams. To graphically illustrate the CI for the average Satisfaction score, create a Multi-Vari chart (with 95% CI Mean Options) using Customer Data.xls. Points correspond to individual data. Markers show a maximum confidence limit of 99%, and an average 95% limit.
Now hypothesis testing will be used to more accurately average satisfaction scores and determine the statistical significance of the results.
Calculation using SigmaXL
Confidence intervals are very important for understanding the data received and making decisions on them. To calculate the CI for a discrete proportion, use SigmaXL> Templates and Calculators> Basic Statistical Templates> 1 confidence interval . Before you find the confidence interval in excel, do the following:
- Open Client Data.xls.
- Press the “Sheet 1” or F4 tab to activate the last worksheet. Click SigmaXL> Statistical Tools> Descriptive Statistics.
- Set the checkbox “Use the entire data table”.
- Click "Next".
- Select “General Satisfaction”, press “Numerical Data Variables” (Y).
- Select “Client Type”, click “Group Category” (X1). The default confidence level is 95%.
- Click OK.
Note that a confidence interval of 95% means: on average, the true parameter of the population (average, standard deviation or proportion) will be in the interval 19 times out of 20. The user will be presented with: 95% confidence interval for each sample. The average value (95% CI). 95% confidence interval for standard deviation (95% CI Sigma - do not confuse this with the Sigma Process quality level).
Statistics and trust levels
The confidence interval is not a number in which the true value of the parameter is found with accuracy. Indeed, a random variable can theoretically take all possible values within the framework of the laws of physics. The confidence interval is actually the area in which the true (unknown) value of the parameter studied in the population is most likely with the probability that is chosen. When using it, the interval is based on the calculation of the confidence threshold, error, and safety factor.
Before determining the confidence interval in excel, determine these elements, which depend on the parameters:
- Variability of the measured characteristics.
- Sample size: the larger it is, the higher the accuracy.
- Sampling method.
- The level of trust is s.
The level of trust is guaranteed assurance. For example, with a confidence level of 90%, this means that a 10% risk will be wrong. As a rule, it is good practice to choose a confidence level of 95%. Thus, the maximum confidence level is greater, the larger the sample size. Margin ratio is an indicator derived directly from the confidence threshold. The table shows some examples for the most common values.
Trust level s | Margin ratio for n> 30 |
80% | 1.28 |
85% | 1.44 |
90% | 1645 |
95% | 1.96 |
96% | 2.05 |
98% | 2,33 |
99% | 2575 |
Indicators for calculation
In the case when you need to evaluate the average value of a population from its sample, determine the confidence interval. It depends on the size of the sample and the law of the variable. The formula for calculating the confidence interval in excel is as follows:
- Lower interval limit = average mileage - field coefficient * standard error.
- Upper range limit = approximate mean + field coefficient * standard error.
- The value of t will depend on the sample size: n> 30: the safety factor of the normal law, called z. n <30: safety factor called t for n-1.
In this situation, the corresponding units themselves are averages. The researcher will need to know the standard deviation not from the initial and individual observations, but from the means that are calculated on the basis of them. This deviation has a name - standard error of the mean.
Error bars
Data variability representations are used in graphs to indicate measurement error or uncertainty. They give a general idea of how accurate the measurement is, or, conversely, how far from the reported true value and are presented in the form of error bars. They represent one standard deviation of uncertainty, one standard error, or a certain confidence interval (for example, 95% interval). These values do not coincide, therefore, the selected measure should be indicated in the graph or in the text.
Error bars can be used to compare two values if statistically significant conditions are met. The error bars indicate the acceptability of the correspondence of the function, i.e. how well it describes the data. Scientific works in experimental sciences include errors on all graphs, although the practice is somewhat different and each researcher has his own style of errors.
Error bars can be used as a direct manipulation interface for controlling probabilistic algorithms for rough calculation. Error bars can be expressed in plus or minus signs (±). Plus is the upper limit, and minus is the lower limit of the error.
Critical value calculator
For the correct determination of CI, there are online calculators that greatly simplify the work. Begin the determination process with the selection of data. It is the basis of all research. Reliable sampling helps you make business decisions with confidence. The first question that needs to be solved is the correct definition of the target group, it is of decisive importance. If the researcher conducts a survey with people outside this group, it is impossible to successfully complete the task. The next step is to decide how many people are needed for the interview.

Experts know that a small representative sample will reflect the opinions and behavior of the group from which it was composed. The larger the sample, the more accurately it represents the target group. However, the rate of improvement in accuracy decreases with increasing sample size. For example, an increase from 250 to 1000 doubles the accuracy. Decide on the size of the sample based on such factors as: available time, budget and the required degree of accuracy.
There are three factors that determine the size of the MDI for this confidence level:
- sample size;
- percentage of the sample;
- population size.
If 99% of the respondents said “Yes” and 1% said “No”, the probability of error is small, regardless of the size of the sample. However, if the percentages are 51 and 49%, the probability of error is much higher. It is easier to be sure of the extreme answers than the average. When determining the sample size required for a given level of accuracy, the worst percentage (50%) should be used.
Below is the formula for calculating the confidence interval in excel of the sample size of the online calculator.
Confidence interval calculations suggest that there is a genuine random sample of the corresponding population. If the survey is not random, you cannot rely on intervals. Non-random samples usually arise due to flaws in the procedure.
Create line charts
Creating a confidence interval chart in Excel is relatively simple. First create your line chart. Then, with the selected row selected, Chart Tools> Layout> Error Panel> Advanced Panel Options. In the pop-up menu that appears, you can either select the positive or negative error panels, or both. You can select a style and select the amount you want to display. This can be a fixed value, percentage, standard deviation, or custom range.
If the data has a default standard deviation for each point, select the user one and click the "Define Value" button. Then another pop-up menu appears and you can select a range of cells for both positive and negative panels.
The order of construction of the diagram:
- Prepare data. First, in addition to the average values, you will need to calculate the standard deviation (or error).
- Then, in line 4, you need to calculate the upper limit of the group, that is, for B4, the calculation will be: = B2 + B3 In line 5, you need to calculate the lower limit of the range, i.e. for B5, the calculation will be: = B2-B4
- Create a schedule. Select rows 1, 2, 4, and 5 of the table, and then click Insert> Graph> Line Chart. Excel will create a line chart.
- Remove legend and grid lines.
- Then right-click the upper group of ranges and select "Change Chart Type".
- Format confidence ranges. To finish the diagram, simply format the top series with a blue fill (according to the blue line), and the bottom series with a white fill.
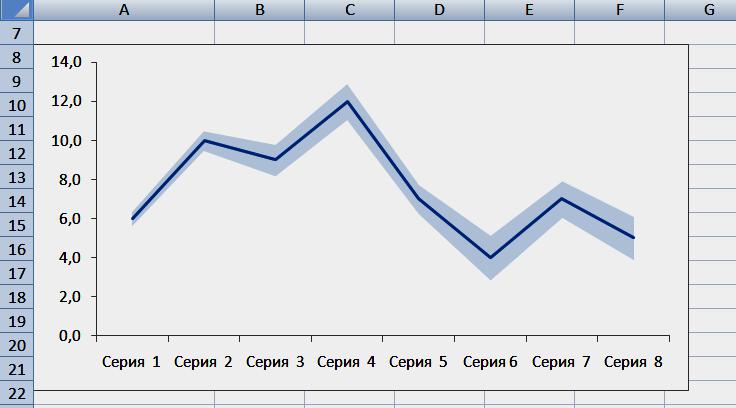
It is easy to see error limits in this diagram, however if there is a lot of data, the view will be erratic. At first glance, the confidence limit is much more obvious, given the average value of the sample, and it will become more stringent as the number of samples increases.